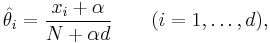Additive smoothing

In statistics, additive smoothing, also called Laplace smoothing[1] (not to be confused with Laplacian smoothing), or Lidstone smoothing, is a technique used to smooth categorical data. Given an observation x = (x1, …, xd) from a multinomial distribution with N trials and parameter vector θ = (θ1, …, θd), a "smoothed" version of the data gives the estimator:

\hat\theta_i= \frac{x_i %2B \alpha}{N %2B \alpha d} \qquad (i=1,\ldots,d),

where α > 0 is the smoothing parameter (α = 0 corresponds to no smoothing). Additive smoothing is a type of shrinkage estimator, as the resulting estimate will be between the empirical estimate xi/n, and the uniform probability 1/d. Using Laplace's rule of succession, some authors have argued that α should be 1 (in which case the term add-one smoothing[2][3] is also used), though in practice a smaller value is typically chosen.

From a Bayesian point of view, this corresponds to the expected value of the posterior distribution, using a Dirichlet distribution with parameter α as a prior.

Contents

Applications

Statistical language modelling

In a bag of words model of natural language processing and information retrieval, the data consists of the number of occurrences of each word in a document. Additive smoothing allows the assignment of non-zero probabilities to words which do not occur in the sample.

Chen & Goodman (1996) empirically compare additive smoothing to a variety of other techniques, using both α fixed at one and a more general value.

See also

References

  1. ^ C.D. Manning, P. Raghavan and M. Schütze (2008). Introduction to Information Retrieval. Cambridge University Press, p. 240.
  2. ^ Jurafsky, Daniel; Martin, James H. (June 2008). Speech and Language Processing (2nd ed.). Prentice Hall. pp. 132. ISBN 978-0131873216. 
  3. ^ Russell, Stuart; Norvig, Peter (2010). Artificial Intelligence: A Modern Approach (2nd ed.). Pearson Education, Inc.. pp. 863. 

External links